How do populations of neurons encode movement?#
This notebook will help you regenerate some of the figures in Churchland & Cunningham et al., 2012, as well as understand how changing parameters in the analysis change these visualizations (and how we interpret them).
Setup#
First, we’ll clone and install a super useful jPCA package, written by Benjamin Antin at Columbia University. If you’ve already installed this package, the cell below will simply import it.
try:
import jPCA
print('jPCA imported.')
except:
!git clone https://github.com/bantin/jPCA.git
%cd jPCA
!pip install .
jPCA imported.
After installing and/or importing the jPCA package, we also need to import numpy and matplotlib.pyplot.
import numpy as np
import matplotlib.pyplot as plt
print('Packages imported.')
Packages imported.
Load data and inspect it#
Below, we’ll use the helper function load_churchland_data to load the Churchland & Cunningham et al. (2012) data that is hosted on the Churchland lab website. We’ll also first take a look at one of the objects, data.
from dandi.dandiapi import DandiAPIClient
dandiset_id = '000070' # ephys dataset from Shenoy lab
filepath = 'sub-Jenkins/sub-Jenkins_ses-20090916_behavior+ecephys.nwb' # one file from one monkeyb
with DandiAPIClient() as client:
asset = client.get_dandiset(dandiset_id, 'draft').get_asset_by_path(filepath)
s3_url = asset.get_content_url(follow_redirects=1, strip_query=True)
print(s3_url)
https://dandiarchive.s3.amazonaws.com/blobs/2dd/66a/2dd66ad9-e7d9-4b96-9de1-4a90ca416048
import urllib.request
import jPCA
from jPCA.util import load_churchland_data, plot_projections
# URL of data to download
data_url = 'https://github.com/nwb4edu/development/blob/0f181c8092d79278fcb0320d9f53bc33fbb0df85/exampleData.mat?raw=true'
# Get the data and save it locally as "sleep_data.txt"
path, headers = urllib.request.urlretrieve(data_url, './exampleData.mat')
data, times = load_churchland_data(path)
print(len(data)) # Show the length of data
data[:10] # Look at the first 10 entries in data
---------------------------------------------------------------------------
KeyboardInterrupt Traceback (most recent call last)
Cell In[4], line 9
6 data_url = 'https://github.com/nwb4edu/development/blob/0f181c8092d79278fcb0320d9f53bc33fbb0df85/exampleData.mat?raw=true'
8 # Get the data and save it locally as "sleep_data.txt"
----> 9 path, headers = urllib.request.urlretrieve(data_url, './exampleData.mat')
11 data, times = load_churchland_data(path)
13 print(len(data)) # Show the length of data
File ~/anaconda3/envs/jb/lib/python3.11/urllib/request.py:270, in urlretrieve(url, filename, reporthook, data)
267 reporthook(blocknum, bs, size)
269 while True:
--> 270 block = fp.read(bs)
271 if not block:
272 break
File ~/anaconda3/envs/jb/lib/python3.11/http/client.py:465, in HTTPResponse.read(self, amt)
462 if self.length is not None and amt > self.length:
463 # clip the read to the "end of response"
464 amt = self.length
--> 465 s = self.fp.read(amt)
466 if not s and amt:
467 # Ideally, we would raise IncompleteRead if the content-length
468 # wasn't satisfied, but it might break compatibility.
469 self._close_conn()
File ~/anaconda3/envs/jb/lib/python3.11/socket.py:705, in SocketIO.readinto(self, b)
703 while True:
704 try:
--> 705 return self._sock.recv_into(b)
706 except timeout:
707 self._timeout_occurred = True
File ~/anaconda3/envs/jb/lib/python3.11/ssl.py:1278, in SSLSocket.recv_into(self, buffer, nbytes, flags)
1274 if flags != 0:
1275 raise ValueError(
1276 "non-zero flags not allowed in calls to recv_into() on %s" %
1277 self.__class__)
-> 1278 return self.read(nbytes, buffer)
1279 else:
1280 return super().recv_into(buffer, nbytes, flags)
File ~/anaconda3/envs/jb/lib/python3.11/ssl.py:1134, in SSLSocket.read(self, len, buffer)
1132 try:
1133 if buffer is not None:
-> 1134 return self._sslobj.read(len, buffer)
1135 else:
1136 return self._sslobj.read(len)
KeyboardInterrupt:
Hmm, why is data a 108-length list of arrays? If we read carefully in the paper, it says:
“In the ‘maze task’ monkeys J and N made both straight reaches and reaches that curved around one or more intervening barriers. This task was beneficial because of the large variety of different reaches that could be evoked. Typically we used 27 conditions: each providing a particular arrangement of target and barriers. Monkey J performed the task for four different sets of 27 conditions, resulting in four datasets (J1 through J4). For the monkey J-array and N-array datasets, 108 conditions were presented in the same recording session.”
There are four different sets of 27 conditions (giving 108 total), each a different arrangement of a target and barrier. Each of the arrays within contains a time x neuron matrix for each condition (hereafter, for clarity, we’ll call these trials. We can inspect the first array to see how many neurons there are.
data
[array([[1.60276178, 3.62279645, 1.51476444, ..., 5.60466456, 8.12611812,
4.51181022],
[1.55470078, 3.61949889, 1.52247338, ..., 5.8348096 , 8.39029125,
4.49137067],
[1.50889271, 3.6006078 , 1.51828573, ..., 6.10419168, 8.69046855,
4.46007445],
...,
[4.12529142, 0.82163592, 0. , ..., 0.93349805, 4.08401884,
2.88854864],
[4.45614688, 0.75939308, 0. , ..., 1.02900484, 3.93844586,
2.50915528],
[4.81611363, 0.71241948, 0. , ..., 1.11870277, 3.78184694,
2.23669761]]),
array([[1.98988481e+00, 9.18115783e+00, 4.84613933e-01, ...,
8.29134273e+00, 1.28676193e+01, 5.34669479e+00],
[2.03938737e+00, 8.95338260e+00, 4.71113281e-01, ...,
8.66122138e+00, 1.29588883e+01, 5.27734065e+00],
[2.11567852e+00, 8.73625972e+00, 4.36420133e-01, ...,
9.01331021e+00, 1.30878842e+01, 5.12815676e+00],
...,
[0.00000000e+00, 8.89741886e-01, 1.20710063e-01, ...,
1.77465655e+00, 5.54310886e+00, 4.64197132e+00],
[4.34632238e-01, 8.58363468e-01, 5.94563715e-02, ...,
1.77712679e+00, 5.20989508e+00, 4.28237550e+00],
[1.23498659e+00, 8.28295046e-01, 1.18584586e-02, ...,
1.75649494e+00, 4.79042602e+00, 3.98363834e+00]]),
array([[ 1.60373245, 10.15764322, 0.29813424, ..., 6.96855588,
8.28129753, 3.90105099],
[ 1.569838 , 10.021134 , 0.31419016, ..., 7.28878381,
8.51076048, 3.937435 ],
[ 1.55323424, 9.75734348, 0.32486749, ..., 7.62972653,
8.8555404 , 3.99531886],
...,
[ 0.77569014, 1.61741704, 0.26314808, ..., 2.36269075,
5.84946381, 6.43682085],
[ 1.31849522, 1.61624415, 0.23164867, ..., 2.23056838,
5.62593022, 6.4016482 ],
[ 2.02338781, 1.62394422, 0.21108832, ..., 2.10164688,
5.39176039, 6.42803701]]),
array([[2.72760539e+00, 2.88838501e+01, 0.00000000e+00, ...,
8.51932370e+00, 1.11985675e+01, 4.52686021e+00],
[2.67390640e+00, 2.84223262e+01, 2.53716630e-03, ...,
8.87067363e+00, 1.15797916e+01, 4.22883051e+00],
[2.60115725e+00, 2.77449432e+01, 9.19432870e-03, ...,
9.22141101e+00, 1.20100251e+01, 3.87817751e+00],
...,
[1.32059867e+01, 0.00000000e+00, 2.17196058e-02, ...,
2.18950438e+00, 8.22869141e+00, 1.62000847e+01],
[1.31175366e+01, 0.00000000e+00, 1.81035530e-02, ...,
2.27029301e+00, 7.68207040e+00, 1.45853136e+01],
[1.29664334e+01, 0.00000000e+00, 1.43236629e-02, ...,
2.30341582e+00, 7.07254659e+00, 1.30476296e+01]]),
array([[ 3.41652625, 15.30420543, 0.31560335, ..., 5.55989529,
7.89834632, 2.55235159],
[ 3.44291429, 14.94753565, 0.29931779, ..., 5.78522773,
8.05902305, 2.51652769],
[ 3.4348078 , 14.41107245, 0.27380366, ..., 6.09202126,
8.30579099, 2.58677391],
...,
[20.97243685, 0. , 0. , ..., 1.0827491 ,
5.51890839, 18.01749614],
[21.19895812, 0. , 0. , ..., 1.29116673,
5.3266248 , 17.86940981],
[21.22406973, 0. , 0. , ..., 1.46901007,
5.12274536, 17.59725915]]),
array([[4.03923418e+00, 1.36332909e+01, 0.00000000e+00, ...,
5.44131703e+00, 8.48576516e+00, 3.06348630e+00],
[4.07191047e+00, 1.32253702e+01, 2.53716630e-03, ...,
5.64141161e+00, 8.58871439e+00, 3.04405261e+00],
[4.09220598e+00, 1.27503908e+01, 9.19432870e-03, ...,
5.90183520e+00, 8.72992838e+00, 3.11563348e+00],
...,
[1.82841848e+01, 0.00000000e+00, 2.17196058e-02, ...,
6.30578050e-01, 3.96554230e+00, 1.98244539e+01],
[1.83640149e+01, 0.00000000e+00, 1.81035530e-02, ...,
9.15449621e-01, 3.88906459e+00, 1.98647166e+01],
[1.83092114e+01, 0.00000000e+00, 1.43236629e-02, ...,
1.16036934e+00, 3.77210293e+00, 1.96804517e+01]]),
array([[1.6649231 , 1.54846916, 0.23029342, ..., 5.06335567, 9.19511398,
5.04997387],
[1.68467823, 1.52632859, 0.19169466, ..., 5.28183642, 9.49420333,
5.1348521 ],
[1.70369659, 1.4793452 , 0.18148143, ..., 5.55075934, 9.8505357 ,
5.24377644],
...,
[2.31733141, 1.80694326, 0. , ..., 1.35858661, 5.58251028,
5.43404842],
[2.16833113, 1.774965 , 0. , ..., 1.35887535, 5.24024774,
4.80467814],
[2.00670126, 1.74779926, 0. , ..., 1.36631926, 4.90706029,
4.22998486]]),
array([[3.79552599, 3.39280084, 0. , ..., 6.32034651, 5.88440318,
3.85917332],
[3.86538517, 3.28978386, 0. , ..., 6.53654853, 5.98880166,
3.93190762],
[3.97796234, 3.1487481 , 0. , ..., 6.81210714, 6.20658187,
4.04437122],
...,
[3.90025433, 3.0066539 , 0.33077066, ..., 6.35071173, 3.46221117,
4.33747868],
[4.0121167 , 2.94413028, 0.37893628, ..., 5.54029745, 3.62462199,
4.6777363 ],
[4.15470646, 2.8824668 , 0.43859265, ..., 4.82267132, 3.74731782,
5.00949809]]),
array([[4.25736601, 4.40688495, 0. , ..., 5.07081411, 6.62688377,
3.71489383],
[4.32244144, 4.29753924, 0. , ..., 5.28244275, 6.8641511 ,
3.68663197],
[4.4330013 , 4.07015713, 0. , ..., 5.58151686, 7.18845814,
3.6953928 ],
...,
[4.01073048, 3.1942071 , 0.29335473, ..., 6.44955845, 4.349918 ,
4.21620661],
[3.73210996, 3.14390731, 0.32311401, ..., 5.57861995, 4.37063976,
4.09425406],
[3.49415452, 3.10281821, 0.36125002, ..., 4.80957995, 4.34536525,
4.05340816]]),
array([[2.28999702, 7.74126035, 0.07296037, ..., 6.23387879, 9.14562329,
3.11584665],
[2.3060687 , 7.62697086, 0.07916832, ..., 6.56379207, 9.30814884,
3.00823497],
[2.34111484, 7.50059092, 0.08822277, ..., 6.88993767, 9.50221832,
2.89594494],
...,
[2.56678043, 0.66563231, 0. , ..., 1.76669617, 4.02700293,
2.6701241 ],
[2.75769703, 0.64591699, 0. , ..., 1.80855134, 3.81500126,
2.87936864],
[2.96793386, 0.6293154 , 0. , ..., 1.80527546, 3.61018331,
3.18619669]]),
array([[2.22243032, 5.86310697, 0.06353286, ..., 4.0875398 , 6.73371472,
3.60170182],
[2.25003339, 5.61461194, 0.07320199, ..., 4.13303265, 6.84387284,
3.67581931],
[2.265914 , 5.42962795, 0.0814212 , ..., 4.25228074, 7.06619933,
3.79158112],
...,
[4.14736749, 0.28155847, 0.10789361, ..., 4.38130409, 4.52306208,
7.51798279],
[3.38768577, 0.2437706 , 0.10365644, ..., 4.0154636 , 4.41358797,
7.73093106],
[2.71222351, 0.19779762, 0.10204216, ..., 3.69522705, 4.33848476,
7.94926667]]),
array([[ 1.75367305, 10.30253536, 0. , ..., 4.76537221,
5.43230703, 2.93712154],
[ 1.74630018, 10.07630737, 0. , ..., 4.89012279,
5.53349158, 2.97229503],
[ 1.69146311, 9.79758433, 0. , ..., 5.07916612,
5.74163086, 3.0560736 ],
...,
[ 8.78780058, 0.51406829, 0.66561513, ..., 3.79634663,
2.80072673, 4.33355048],
[ 7.65555519, 0.5100773 , 0.71488696, ..., 3.49212057,
2.9781718 , 4.5230533 ],
[ 6.5348606 , 0.50013062, 0.7771565 , ..., 3.22302843,
3.1442675 , 4.84313429]]),
array([[1.45822298, 1.4038674 , 0.92141125, ..., 4.80667142, 8.07372409,
4.15168228],
[1.33708779, 1.369454 , 0.93998289, ..., 4.94590039, 8.38556846,
4.15988013],
[1.2296963 , 1.33724842, 0.97645323, ..., 5.16257476, 8.76521161,
4.18467935],
...,
[1.73311544, 2.02098164, 0. , ..., 0.76630267, 4.1470332 ,
3.63341392],
[2.09587455, 1.91890652, 0. , ..., 0.82959351, 4.03811835,
3.34394868],
[2.55664619, 1.82757726, 0. , ..., 0.92376486, 3.90849472,
3.15590811]]),
array([[4.25489158, 2.2333193 , 0.36996591, ..., 4.54661333, 8.77507794,
3.8082854 ],
[4.35992342, 2.13523051, 0.39126254, ..., 4.74093078, 8.91341408,
3.95202798],
[4.48601521, 2.01835732, 0.41867211, ..., 5.00097447, 9.07736519,
4.20487487],
...,
[8.05659481, 1.50917466, 0.07725393, ..., 2.05013318, 3.48998356,
9.86991491],
[7.57380595, 1.3843801 , 0.05474612, ..., 1.87889377, 3.53598455,
9.78707421],
[7.08010562, 1.27336851, 0.03671255, ..., 1.74452815, 3.48073192,
9.65169941]]),
array([[3.25409131, 3.90045749, 0.10437125, ..., 5.6191784 , 7.83541088,
4.73721557],
[3.27841126, 3.78283811, 0.08835427, ..., 5.89553278, 7.92636852,
4.80289346],
[3.30685242, 3.55131811, 0.09565402, ..., 6.24436529, 8.05674915,
4.90276256],
...,
[7.92252724, 2.13717222, 0. , ..., 2.4409555 , 3.64309195,
8.7969883 ],
[7.45187619, 2.01801197, 0. , ..., 2.15925483, 3.66908537,
8.35897052],
[6.96073648, 1.91333168, 0. , ..., 1.93002863, 3.63382 ,
7.911418 ]]),
array([[3.97866997e+00, 2.65780358e+01, 1.34693114e-02, ...,
5.30774374e+00, 8.16345058e+00, 4.71293781e+00],
[3.92536697e+00, 2.60336090e+01, 1.99575768e-02, ...,
5.56217007e+00, 8.48541707e+00, 4.55802081e+00],
[3.87711828e+00, 2.54265805e+01, 2.76546376e-02, ...,
5.89482327e+00, 8.96385394e+00, 4.39200621e+00],
...,
[1.22856272e+01, 0.00000000e+00, 3.85142694e-03, ...,
2.42997324e+00, 1.01212222e+01, 1.30767225e+01],
[1.19057554e+01, 0.00000000e+00, 0.00000000e+00, ...,
2.39393750e+00, 9.54856083e+00, 1.14896825e+01],
[1.15994328e+01, 0.00000000e+00, 0.00000000e+00, ...,
2.34332087e+00, 8.98188226e+00, 1.00576055e+01]]),
array([[5.78180347e+00, 1.24273094e+01, 8.48301657e-02, ...,
3.92292240e+00, 6.65332623e+00, 4.53686872e+00],
[5.84942413e+00, 1.21151390e+01, 1.10475821e-01, ...,
4.15463021e+00, 6.82380802e+00, 4.49961767e+00],
[5.89954086e+00, 1.16717266e+01, 1.32687002e-01, ...,
4.47591234e+00, 7.08684178e+00, 4.49069089e+00],
...,
[2.48285674e+01, 7.16746303e-01, 3.12014047e-02, ...,
8.82000289e-01, 5.13507529e+00, 1.97768753e+01],
[2.42346104e+01, 7.11968538e-01, 2.06943818e-02, ...,
1.03977212e+00, 5.15293282e+00, 1.88872957e+01],
[2.35015066e+01, 7.11166825e-01, 9.75073510e-03, ...,
1.17038916e+00, 5.09676736e+00, 1.78665228e+01]]),
array([[ 5.12443559, 13.04651492, 0.05091652, ..., 3.43488765,
8.97304307, 4.24405781],
[ 5.21194438, 12.67348409, 0.06602638, ..., 3.44324733,
9.03239935, 4.22264723],
[ 5.28189248, 12.1925065 , 0.07965902, ..., 3.53066354,
9.12182614, 4.25632136],
...,
[21.02864067, 0. , 0.03530874, ..., 2.02905498,
5.40267679, 19.17050593],
[20.4544492 , 0. , 0.03083018, ..., 2.15033032,
5.24095704, 18.20334931],
[19.78631255, 0. , 0.0264245 , ..., 2.2564964 ,
5.00620941, 17.20847634]]),
array([[1.38777086, 6.69866761, 0.40593286, ..., 4.84711283, 7.11797523,
3.57711873],
[1.35803988, 6.60315658, 0.40462648, ..., 5.06226378, 7.22890295,
3.58125038],
[1.32480211, 6.51266095, 0.39364844, ..., 5.30112249, 7.3900845 ,
3.60537882],
...,
[3.07132061, 0.2049852 , 0. , ..., 1.71602461, 1.54135429,
3.35045502],
[3.17139205, 0.16934381, 0. , ..., 1.78847837, 1.57852839,
3.37813311],
[3.29377544, 0.14237518, 0. , ..., 1.82556712, 1.66522806,
3.49864026]]),
array([[3.00087168e+00, 4.72361792e+00, 4.74024431e-02, ...,
4.29480212e+00, 5.84036558e+00, 4.44696285e+00],
[3.01314000e+00, 4.65435025e+00, 6.62882392e-02, ...,
4.52522718e+00, 5.98633145e+00, 4.45957194e+00],
[3.02125018e+00, 4.56844432e+00, 8.17333501e-02, ...,
4.83579114e+00, 6.26532858e+00, 4.50095183e+00],
...,
[9.73962453e+00, 0.00000000e+00, 2.40585796e-02, ...,
5.13498969e-01, 5.35515581e+00, 7.04212014e+00],
[9.41572231e+00, 0.00000000e+00, 1.62365342e-02, ...,
5.85226029e-01, 4.98006686e+00, 6.13669266e+00],
[8.98775279e+00, 0.00000000e+00, 8.03138800e-03, ...,
6.67661338e-01, 4.78371131e+00, 5.39733858e+00]]),
array([[3.19509997e+00, 7.06034735e+00, 1.40686536e-01, ...,
2.94645671e+00, 8.71188517e+00, 4.49860281e+00],
[3.18746901e+00, 6.95022800e+00, 1.57585390e-01, ...,
3.17676686e+00, 8.91829738e+00, 4.48168933e+00],
[3.18791428e+00, 6.78063069e+00, 1.68300706e-01, ...,
3.52565657e+00, 9.23233496e+00, 4.47540307e+00],
...,
[8.47279129e+00, 0.00000000e+00, 3.88588954e-03, ...,
1.30588602e+00, 7.35853915e+00, 7.37964104e+00],
[8.23659917e+00, 0.00000000e+00, 0.00000000e+00, ...,
1.20164336e+00, 6.77262746e+00, 6.89081463e+00],
[7.94496763e+00, 0.00000000e+00, 0.00000000e+00, ...,
1.12861721e+00, 6.29599618e+00, 6.45222754e+00]]),
array([[2.19940172, 1.98088344, 0.24767557, ..., 3.60642881, 7.3542422 ,
3.70644404],
[2.23674966, 1.99366614, 0.27783974, ..., 3.80544115, 7.50219938,
3.72811846],
[2.29657281, 1.96595482, 0.31676653, ..., 4.09768519, 7.7296775 ,
3.80369821],
...,
[0.09425223, 1.3394413 , 0.05902881, ..., 1.19785259, 4.37708621,
5.56882634],
[0.07709037, 1.32718927, 0.04799686, ..., 1.15134788, 4.2731897 ,
5.1603122 ],
[0.09162409, 1.31963047, 0.03822359, ..., 1.13103445, 4.1744262 ,
4.90142869]]),
array([[0.96135761, 2.20511121, 0.05393278, ..., 2.98061867, 6.02008901,
4.87765807],
[0.86248433, 2.19959864, 0.05827351, ..., 3.10300856, 6.16505559,
4.88165262],
[0.75584989, 2.14411647, 0.05507524, ..., 3.32435751, 6.40951209,
4.88728879],
...,
[2.49563713, 0.86038449, 0.1524641 , ..., 1.41201953, 4.59752948,
7.27539778],
[2.38478433, 0.8556708 , 0.13869091, ..., 1.37828737, 4.50695071,
6.750338 ],
[2.21720243, 0.85661111, 0.13074626, ..., 1.37099487, 4.45041358,
6.23580454]]),
array([[1.22641474, 2.95840783, 0. , ..., 3.98884661, 6.5163163 ,
3.05823326],
[1.14217731, 2.86712107, 0. , ..., 4.13850478, 6.65828743,
2.99411613],
[1.06110112, 2.68540493, 0. , ..., 4.35598484, 6.89852176,
3.00772725],
...,
[1.09731801, 2.36910253, 0.42007969, ..., 1.79745415, 4.64747809,
7.92206627],
[0.98389337, 2.34266681, 0.44607805, ..., 1.73855544, 4.57382821,
7.61844541],
[0.84326355, 2.31674102, 0.48166087, ..., 1.69705222, 4.50907122,
7.33896333]]),
array([[2.99763072e+00, 1.96323541e+01, 2.70962416e-02, ...,
6.12023266e+00, 9.51782188e+00, 5.50776390e+00],
[3.01299957e+00, 1.91981704e+01, 3.51019058e-02, ...,
6.37624967e+00, 9.69256663e+00, 5.55272046e+00],
[3.03348320e+00, 1.86518567e+01, 4.06874469e-02, ...,
6.68295314e+00, 9.88500327e+00, 5.61556246e+00],
...,
[9.61699427e+00, 9.45329945e-01, 1.78234161e-02, ...,
2.10301337e+00, 5.82217553e+00, 1.96437510e+01],
[9.85833869e+00, 9.37684306e-01, 1.36393100e-02, ...,
2.15995698e+00, 5.57774024e+00, 1.83140321e+01],
[1.00658079e+01, 9.28874445e-01, 9.47277258e-03, ...,
2.18708841e+00, 5.25645669e+00, 1.69463231e+01]]),
array([[3.63537765e+00, 1.19974640e+01, 0.00000000e+00, ...,
4.57322491e+00, 8.09597564e+00, 3.83390805e+00],
[3.54801757e+00, 1.16979356e+01, 2.53716630e-03, ...,
4.85857253e+00, 8.24196395e+00, 3.98482367e+00],
[3.47092627e+00, 1.12132327e+01, 9.19432870e-03, ...,
5.17373947e+00, 8.52425469e+00, 4.26697208e+00],
...,
[1.15367878e+01, 1.30322383e+00, 2.17196058e-02, ...,
1.56675809e+00, 9.78182623e+00, 1.84127366e+01],
[1.15019246e+01, 1.23825087e+00, 1.81035530e-02, ...,
1.58063123e+00, 9.33701840e+00, 1.78079303e+01],
[1.15205752e+01, 1.18518781e+00, 1.43236629e-02, ...,
1.56453236e+00, 8.84754558e+00, 1.71223967e+01]]),
array([[4.22375764e+00, 1.20053314e+01, 0.00000000e+00, ...,
5.65951609e+00, 7.25242349e+00, 5.17238810e+00],
[4.19626761e+00, 1.17045260e+01, 2.53716630e-03, ...,
5.94484749e+00, 7.31411207e+00, 5.29982415e+00],
[4.18205575e+00, 1.12664790e+01, 9.19432870e-03, ...,
6.23023403e+00, 7.50053459e+00, 5.47098149e+00],
...,
[1.27070826e+01, 8.76665488e-01, 2.17196058e-02, ...,
1.44004333e+00, 7.72524469e+00, 1.69800816e+01],
[1.25858782e+01, 8.10825650e-01, 1.81035530e-02, ...,
1.50217462e+00, 7.37971515e+00, 1.61242861e+01],
[1.25028375e+01, 7.53293047e-01, 1.43236629e-02, ...,
1.52833120e+00, 7.05146990e+00, 1.52059384e+01]]),
array([[ 1.7935364 , 11.8475038 , 0.15026386, ..., 6.40275778,
8.93016703, 3.06747581],
[ 1.82836078, 11.69047732, 0.18348271, ..., 6.73682112,
8.85584892, 3.0481358 ],
[ 1.84746314, 11.35864513, 0.21486636, ..., 7.08339677,
8.78648536, 3.08486769],
...,
[ 5.46684262, 0.38420527, 0.05799396, ..., 2.014417 ,
3.63147478, 6.17732637],
[ 5.15763441, 0.40360853, 0.0465939 , ..., 2.04140873,
3.58573012, 5.80276532],
[ 4.80120876, 0.44059979, 0.03515912, ..., 2.02528808,
3.48200588, 5.62369788]]),
array([[ 3.1887287 , 13.25987976, 0.10330944, ..., 5.7571771 ,
7.57066134, 2.54483396],
[ 3.26083993, 12.98290666, 0.10075447, ..., 6.01725922,
7.70705664, 2.53910032],
[ 3.31367473, 12.51428896, 0.09745021, ..., 6.29195401,
7.90675546, 2.63724261],
...,
[11.85584907, 0.24369296, 0. , ..., 2.0945764 ,
4.91962035, 14.42108374],
[11.30509882, 0.26068157, 0. , ..., 2.09934859,
4.92811895, 14.62655123],
[10.67866027, 0.28497589, 0. , ..., 2.07387783,
4.84042528, 14.73909536]]),
array([[3.15976274e+00, 1.33627828e+01, 0.00000000e+00, ...,
6.01220130e+00, 7.06004846e+00, 3.29377499e+00],
[3.23742961e+00, 1.30958731e+01, 2.47132728e-03, ...,
6.24508378e+00, 7.16851245e+00, 3.31466139e+00],
[3.28712602e+00, 1.25559924e+01, 9.14180889e-03, ...,
6.48864923e+00, 7.36829399e+00, 3.40638939e+00],
...,
[1.38482528e+01, 1.48540114e+00, 2.11380192e-02, ...,
2.06552875e+00, 7.33089578e+00, 1.35062266e+01],
[1.33159227e+01, 1.50235705e+00, 1.74831348e-02, ...,
2.09282911e+00, 7.22053490e+00, 1.32997335e+01],
[1.26612043e+01, 1.53072653e+00, 1.36477942e-02, ...,
2.09201713e+00, 6.99832914e+00, 1.30762565e+01]]),
array([[1.49520493, 1.59506504, 0.99953592, ..., 5.65482207, 7.87302478,
4.31856282],
[1.50439763, 1.57291673, 1.00222191, ..., 5.95846767, 8.02387833,
4.3466483 ],
[1.52020623, 1.52113321, 1.04170461, ..., 6.29884278, 8.24312307,
4.39887546],
...,
[0.26336281, 1.55259501, 0.13021132, ..., 1.09891633, 3.84432156,
3.8501816 ],
[0.21135381, 1.50343386, 0.12166742, ..., 1.12203912, 3.84091546,
3.59397446],
[0.17868697, 1.46402991, 0.1230709 , ..., 1.1386711 , 3.79171238,
3.37428807]]),
array([[2.21482573, 4.84385221, 0.07990027, ..., 5.08479568, 7.63274783,
3.73122304],
[2.3090993 , 4.78901263, 0.06633978, ..., 5.31674414, 7.86520884,
3.68613037],
[2.42035024, 4.65308661, 0.05242207, ..., 5.58785983, 8.17305142,
3.66173987],
...,
[2.8886874 , 0.67577859, 0.20823527, ..., 1.19691341, 3.44476475,
7.66422816],
[3.41607815, 0.67449865, 0.19879259, ..., 1.25995568, 3.35859978,
7.8487609 ],
[3.96024996, 0.68183315, 0.19896849, ..., 1.3113419 , 3.29359912,
7.96266972]]),
array([[1.6960728 , 6.53097878, 0.06536701, ..., 5.94256737, 7.52977584,
3.83538249],
[1.77950815, 6.40953005, 0.05839111, ..., 6.19658662, 7.79983803,
3.78179281],
[1.87307874, 6.12083478, 0.04673653, ..., 6.47773945, 8.1665469 ,
3.72368173],
...,
[2.59630336, 1.54977859, 0.07911601, ..., 1.49259129, 5.70029078,
4.71490631],
[3.29044987, 1.54438948, 0.05625324, ..., 1.51749561, 5.46423859,
4.79596847],
[4.00091147, 1.54790133, 0.03995352, ..., 1.53358746, 5.24029925,
4.91344362]]),
array([[4.14344900e+00, 3.13098776e+01, 2.97058345e-02, ...,
5.97579826e+00, 9.41465860e+00, 4.52095065e+00],
[4.16282577e+00, 3.07014303e+01, 3.93151418e-02, ...,
6.30931889e+00, 9.74146054e+00, 4.49821858e+00],
[4.18034259e+00, 2.99769094e+01, 4.82165598e-02, ...,
6.71178293e+00, 1.01461969e+01, 4.48882126e+00],
...,
[1.54630392e+01, 0.00000000e+00, 2.33585146e-02, ...,
1.86302854e+00, 8.03410335e+00, 1.60601763e+01],
[1.53823641e+01, 0.00000000e+00, 2.03937074e-02, ...,
1.89137830e+00, 7.60697017e+00, 1.49559448e+01],
[1.52656250e+01, 0.00000000e+00, 1.75215179e-02, ...,
1.89316128e+00, 7.12497329e+00, 1.39009992e+01]]),
array([[5.47106841e+00, 1.77383393e+01, 0.00000000e+00, ...,
4.86080322e+00, 8.71058382e+00, 4.48338062e+00],
[5.44172802e+00, 1.72134419e+01, 2.53716630e-03, ...,
5.23078611e+00, 8.73548380e+00, 4.61014171e+00],
[5.38501819e+00, 1.64037214e+01, 9.19432870e-03, ...,
5.62187715e+00, 8.84004688e+00, 4.83930663e+00],
...,
[2.87114781e+01, 2.60659787e+00, 2.17196058e-02, ...,
1.40162680e+00, 8.09915509e+00, 1.88956833e+01],
[2.85925713e+01, 2.56302564e+00, 1.81035530e-02, ...,
1.43106849e+00, 7.59630609e+00, 1.80055268e+01],
[2.83435577e+01, 2.52507236e+00, 1.43236629e-02, ...,
1.41391228e+00, 7.12185632e+00, 1.70501641e+01]]),
array([[5.49379538e+00, 1.54838614e+01, 0.00000000e+00, ...,
5.97195677e+00, 8.64852881e+00, 3.49431123e+00],
[5.47158415e+00, 1.50657147e+01, 2.53716630e-03, ...,
6.29931266e+00, 8.70193700e+00, 3.46910706e+00],
[5.44408459e+00, 1.44185017e+01, 9.19432870e-03, ...,
6.61295390e+00, 8.84319030e+00, 3.52772659e+00],
...,
[2.29032784e+01, 1.72711834e+00, 2.17196058e-02, ...,
1.78542445e+00, 9.00181579e+00, 1.72656980e+01],
[2.26583775e+01, 1.68333619e+00, 1.81035530e-02, ...,
1.81133256e+00, 8.54638115e+00, 1.67636696e+01],
[2.23780833e+01, 1.64961495e+00, 1.43236629e-02, ...,
1.79066346e+00, 8.05573491e+00, 1.61698982e+01]]),
array([[2.36021705e+00, 1.15408184e+01, 1.33215346e-01, ...,
6.58754187e+00, 8.77432756e+00, 3.07811738e+00],
[2.43620882e+00, 1.13165972e+01, 1.46324151e-01, ...,
6.86413135e+00, 8.90071867e+00, 3.02925226e+00],
[2.50999407e+00, 1.09916806e+01, 1.53613189e-01, ...,
7.14688064e+00, 9.06759014e+00, 2.99865992e+00],
...,
[5.42393472e+00, 0.00000000e+00, 1.93964596e-02, ...,
2.02198748e+00, 4.35205200e+00, 3.66963952e+00],
[5.29274125e+00, 0.00000000e+00, 1.47763697e-02, ...,
2.06837095e+00, 4.17548846e+00, 3.72531100e+00],
[5.13974264e+00, 0.00000000e+00, 9.78354243e-03, ...,
2.07847283e+00, 3.98809151e+00, 3.91975167e+00]]),
array([[2.11515965e+00, 1.14137872e+01, 4.51919862e-03, ...,
6.49731848e+00, 1.06353193e+01, 3.61899867e+00],
[2.11652550e+00, 1.11805178e+01, 1.42117838e-02, ...,
6.72916255e+00, 1.05993703e+01, 3.65863697e+00],
[2.11800928e+00, 1.09554890e+01, 2.14056465e-02, ...,
6.97104845e+00, 1.05455438e+01, 3.74472638e+00],
...,
[3.78188191e+00, 3.98300530e-01, 3.09664448e-02, ...,
1.16726621e+00, 3.74569771e+00, 1.04806507e+01],
[3.41155602e+00, 3.61230545e-01, 2.70267239e-02, ...,
1.35832272e+00, 3.45915741e+00, 1.02390948e+01],
[3.02367182e+00, 3.28136325e-01, 2.32779064e-02, ...,
1.50912528e+00, 3.18403548e+00, 1.00616124e+01]]),
array([[2.95345115e+00, 1.36736740e+01, 8.44528260e-02, ...,
7.21628039e+00, 1.21272168e+01, 3.32314367e+00],
[2.98213303e+00, 1.34770603e+01, 8.92205908e-02, ...,
7.43152303e+00, 1.21999120e+01, 3.25684395e+00],
[3.03032449e+00, 1.32179127e+01, 8.85302061e-02, ...,
7.64573424e+00, 1.22937933e+01, 3.20359701e+00],
...,
[3.59517297e+00, 0.00000000e+00, 1.42286127e-02, ...,
1.66274605e+00, 7.51272230e+00, 7.52233587e+00],
[3.29552877e+00, 0.00000000e+00, 1.31513234e-02, ...,
1.81817562e+00, 6.85879145e+00, 7.15228077e+00],
[3.00727663e+00, 0.00000000e+00, 1.18659823e-02, ...,
1.93583554e+00, 6.21835719e+00, 6.93685832e+00]]),
array([[1.45083369, 5.19473432, 0.99856148, ..., 7.56992812, 9.18562254,
3.99199475],
[1.3874268 , 5.12344289, 1.00445175, ..., 7.85306545, 9.41066079,
3.98503596],
[1.31823948, 4.99808232, 1.03062165, ..., 8.1287153 , 9.67396251,
4.00485996],
...,
[4.26643339, 1.70177242, 0.05217733, ..., 1.2994765 , 4.14844878,
4.87226881],
[4.33674235, 1.62514732, 0.04843383, ..., 1.38626102, 3.97709736,
4.56263727],
[4.42527984, 1.56420634, 0.04978247, ..., 1.45495498, 3.78231361,
4.32297136]]),
array([[ 3.74249695, 6.58107845, 0.06421498, ..., 6.62018952,
6.777544 , 3.08631326],
[ 3.83579299, 6.4501112 , 0.06848712, ..., 6.68268252,
7.10370097, 3.09663436],
[ 3.89593965, 6.35199516, 0.06672264, ..., 6.80281585,
7.54605677, 3.2079346 ],
...,
[21.02979328, 2.99055031, 0.02743598, ..., 6.88273964,
6.54333978, 5.43787532],
[21.06326158, 2.69092469, 0.02796466, ..., 6.03490607,
6.28133236, 5.16528269],
[20.81793362, 2.42254333, 0.02853441, ..., 5.30882815,
6.03288143, 4.98317765]]),
array([[ 3.66096145, 11.25379698, 0. , ..., 6.49700534,
6.61127461, 3.39594511],
[ 3.79211182, 11.15791179, 0. , ..., 6.58961224,
6.76221978, 3.36081376],
[ 3.87771498, 11.09443608, 0. , ..., 6.72931891,
6.97890933, 3.38409687],
...,
[22.15024341, 1.65790259, 0.20670073, ..., 6.51855351,
3.52205454, 5.54225004],
[21.99863739, 1.36200078, 0.2180504 , ..., 5.71459667,
3.59567449, 5.54423293],
[21.53081294, 1.11054621, 0.23290841, ..., 5.0206471 ,
3.62810197, 5.5504227 ]]),
array([[2.69505829e+00, 4.64116161e+00, 2.47714534e-01, ...,
5.00414885e+00, 7.57980492e+00, 3.62323158e+00],
[2.76323507e+00, 4.57496781e+00, 2.52817542e-01, ...,
5.23794087e+00, 7.82766298e+00, 3.67883371e+00],
[2.86198162e+00, 4.47476463e+00, 2.67400447e-01, ...,
5.52749703e+00, 8.15297419e+00, 3.78580193e+00],
...,
[4.50933030e-01, 1.66026471e+00, 2.31401703e-03, ...,
1.09300363e+00, 6.65094644e+00, 4.97810435e+00],
[4.37652142e-01, 1.63357480e+00, 0.00000000e+00, ...,
1.10110893e+00, 6.40170274e+00, 4.70997527e+00],
[4.53147239e-01, 1.61323801e+00, 0.00000000e+00, ...,
1.12058997e+00, 6.11867530e+00, 4.58348178e+00]]),
array([[1.32868115, 2.12926815, 0. , ..., 4.09773444, 5.30060277,
3.05137978],
[1.32861755, 2.07927585, 0. , ..., 4.36522497, 5.62684086,
2.87298235],
[1.33809028, 1.99189251, 0. , ..., 4.6801013 , 6.1063259 ,
2.73096118],
...,
[0.53948484, 2.50920684, 0.0324228 , ..., 1.57756252, 6.98234852,
6.4339376 ],
[0.84910785, 2.47719282, 0.02986112, ..., 1.57858013, 6.75925197,
6.26800439],
[1.1696554 , 2.44401045, 0.02740604, ..., 1.55656848, 6.5662749 ,
6.12952306]]),
array([[1.83026658, 2.89786648, 0.01238875, ..., 3.42659485, 7.43596097,
2.78010558],
[1.87113689, 2.85129248, 0.0179895 , ..., 3.63794495, 7.71135873,
2.70572722],
[1.93228989, 2.75770974, 0.0208503 , ..., 3.90003921, 8.07521642,
2.71093846],
...,
[0. , 2.57867877, 0.01578481, ..., 1.44998852, 6.80591886,
6.47795476],
[0.19124066, 2.54586221, 0.01243166, ..., 1.46874355, 6.38811294,
6.17814791],
[0.47813047, 2.51529999, 0.00917329, ..., 1.46891848, 6.02969223,
5.97095453]]),
array([[1.9416086 , 2.42133606, 0.86338133, ..., 5.35384858, 6.70080868,
4.29013198],
[1.97087321, 2.39035427, 0.85686047, ..., 5.62125283, 6.96060418,
4.32368153],
[2.01667653, 2.31033224, 0.88166271, ..., 5.92844358, 7.34330331,
4.41364172],
...,
[0.0764734 , 1.57251631, 0. , ..., 1.30439539, 5.15303171,
6.09566153],
[0.03649258, 1.54394196, 0. , ..., 1.31405876, 5.05803727,
5.32855955],
[0.02860991, 1.52325085, 0. , ..., 1.31954585, 4.95890566,
4.6888808 ]]),
array([[4.50264575, 3.0473958 , 0. , ..., 3.77664342, 4.82276017,
3.96891115],
[4.6036379 , 2.9122038 , 0. , ..., 3.99162882, 5.09288913,
4.05945098],
[4.76084157, 2.71150284, 0. , ..., 4.29818973, 5.46867731,
4.20755552],
...,
[3.57022609, 3.78392319, 0.18609013, ..., 4.91904395, 3.26560234,
5.9342189 ],
[3.53519208, 3.69620776, 0.21343123, ..., 4.28930491, 3.51358813,
5.87994697],
[3.52373134, 3.61139404, 0.2468252 , ..., 3.72814995, 3.69477896,
5.89139005]]),
array([[4.57574732, 4.25799215, 0. , ..., 4.68823483, 7.15041235,
3.78997903],
[4.70575195, 4.18347285, 0. , ..., 4.9026551 , 7.33874228,
3.82085302],
[4.88357416, 3.98472463, 0. , ..., 5.18536445, 7.57254528,
3.89925563],
...,
[5.04012499, 3.05028925, 1.04576628, ..., 4.463408 , 4.08777883,
7.09953877],
[4.89375669, 2.99530784, 1.12774975, ..., 3.92522752, 4.12723537,
7.27925035],
[4.73680137, 2.94769843, 1.23111488, ..., 3.44807694, 4.09088263,
7.38160692]]),
array([[2.15897947, 9.8154201 , 0.09372694, ..., 4.52404371, 7.91885541,
2.82098138],
[2.21849681, 9.59948343, 0.09782157, ..., 4.75374915, 7.95619055,
2.72877097],
[2.2565024 , 9.32554096, 0.09495996, ..., 5.04022641, 8.06832556,
2.65361031],
...,
[8.10100998, 0.48622914, 0.01311323, ..., 1.84282486, 4.91192026,
4.20862197],
[7.73921621, 0.47653304, 0.01283395, ..., 1.8454342 , 4.86655246,
3.87443165],
[7.30570311, 0.47197036, 0.01224652, ..., 1.83171936, 4.75780871,
3.82232469]]),
array([[3.34328418e+00, 1.17676774e+01, 4.71686174e-02, ...,
5.35679864e+00, 5.57100418e+00, 2.42559063e+00],
[3.44503015e+00, 1.15188923e+01, 6.59448226e-02, ...,
5.64701765e+00, 5.69181812e+00, 2.41766917e+00],
[3.51481884e+00, 1.11431126e+01, 8.12708848e-02, ...,
5.96618530e+00, 5.92659355e+00, 2.52423146e+00],
...,
[1.48698204e+01, 1.08233972e+00, 2.36514707e-02, ...,
1.61866006e+00, 3.62240073e+00, 1.69374748e+01],
[1.42418312e+01, 1.07448057e+00, 1.58485509e-02, ...,
1.65756834e+00, 3.68645950e+00, 1.70149995e+01],
[1.34893907e+01, 1.07553825e+00, 7.65736131e-03, ...,
1.66532770e+00, 3.76341391e+00, 1.69507556e+01]]),
array([[ 2.67821417, 13.42372225, 0.02433626, ..., 3.09999727,
5.6052177 , 3.23921901],
[ 2.73206453, 13.06749136, 0.04269307, ..., 3.24568961,
5.7284136 , 3.30866723],
[ 2.74270472, 12.42984685, 0.05889785, ..., 3.46154202,
5.97174008, 3.44194659],
...,
[13.83799851, 1.11828423, 0.16196403, ..., 1.90356155,
5.63506374, 14.55483055],
[13.04943502, 1.13274905, 0.16608312, ..., 1.90148362,
5.56961723, 14.68698735],
[12.15317577, 1.15184345, 0.17248938, ..., 1.88802575,
5.4969095 , 14.77139523]]),
array([[3.74080213e+00, 2.46883419e+01, 0.00000000e+00, ...,
6.66515966e+00, 1.10044649e+01, 3.43306022e+00],
[3.67301181e+00, 2.41141611e+01, 2.53716630e-03, ...,
6.94676547e+00, 1.12694604e+01, 3.14510576e+00],
[3.59347449e+00, 2.33893523e+01, 9.19432870e-03, ...,
7.27525504e+00, 1.15971251e+01, 2.86037778e+00],
...,
[1.48293975e+01, 7.35671159e-01, 2.17196058e-02, ...,
2.27595728e+00, 8.77528208e+00, 1.51261496e+01],
[1.43519347e+01, 7.32073822e-01, 1.81035530e-02, ...,
2.30843876e+00, 8.18236738e+00, 1.36501256e+01],
[1.38897394e+01, 7.24610080e-01, 1.43236629e-02, ...,
2.31214774e+00, 7.54769369e+00, 1.23482067e+01]]),
array([[4.51133173e+00, 2.09269762e+01, 0.00000000e+00, ...,
3.75794269e+00, 7.13707745e+00, 4.36162369e+00],
[4.51775593e+00, 2.03410609e+01, 2.53716630e-03, ...,
3.86091994e+00, 7.46289994e+00, 4.22542083e+00],
[4.50345319e+00, 1.94842513e+01, 9.19432870e-03, ...,
4.05525734e+00, 7.88495047e+00, 4.07533153e+00],
...,
[1.98246859e+01, 7.13723674e-01, 2.17196058e-02, ...,
1.88511696e+00, 5.94574972e+00, 1.64070649e+01],
[1.92637503e+01, 7.15958312e-01, 1.81035530e-02, ...,
1.99609969e+00, 5.73556571e+00, 1.55607050e+01],
[1.86159993e+01, 7.21516413e-01, 1.43236629e-02, ...,
2.08674975e+00, 5.51692897e+00, 1.46869098e+01]]),
array([[3.99564552e+00, 2.17696806e+01, 0.00000000e+00, ...,
4.75447331e+00, 6.80027149e+00, 3.39785212e+00],
[4.01523751e+00, 2.13905609e+01, 2.53716630e-03, ...,
4.87861470e+00, 7.02366106e+00, 3.27109931e+00],
[4.00082658e+00, 2.07551246e+01, 9.19432870e-03, ...,
5.07768521e+00, 7.33883204e+00, 3.20833708e+00],
...,
[1.96315321e+01, 2.63834234e-01, 2.17196058e-02, ...,
1.96570686e+00, 5.61243417e+00, 1.53551635e+01],
[1.90122689e+01, 2.95282125e-01, 1.81035530e-02, ...,
2.07569981e+00, 5.53906167e+00, 1.40827962e+01],
[1.83018652e+01, 3.41108620e-01, 1.43236629e-02, ...,
2.16501977e+00, 5.41123008e+00, 1.29449909e+01]]),
array([[1.57207172, 6.19840013, 0.27291674, ..., 5.91585499, 9.25515762,
3.61493048],
[1.54349144, 6.10561019, 0.273218 , ..., 6.15112605, 9.32635988,
3.67897951],
[1.5159126 , 5.97673456, 0.2635708 , ..., 6.38537128, 9.42560506,
3.7956866 ],
...,
[3.23900688, 0.38748753, 0. , ..., 1.66261745, 2.66476343,
4.23968046],
[3.40517952, 0.36749353, 0. , ..., 1.72813558, 2.60362273,
4.22643891],
[3.60357135, 0.35645421, 0. , ..., 1.76272796, 2.5308582 ,
4.32764442]]),
array([[2.99763592, 4.21859113, 0. , ..., 3.86406795, 7.04997428,
5.0459779 ],
[2.96540242, 4.12025496, 0. , ..., 4.1685265 , 7.38252215,
4.96299334],
[2.93577237, 4.01782511, 0. , ..., 4.59804212, 7.86399711,
4.86585544],
...,
[8.07341909, 0.06373871, 0.03792122, ..., 2.8212614 , 8.14131967,
9.75202597],
[7.66650456, 0. , 0.03588885, ..., 2.40223413, 7.64822276,
9.00888236],
[7.23770398, 0. , 0.03409742, ..., 2.05139516, 7.23349955,
8.19527911]]),
array([[2.80100784e+00, 4.39624488e+00, 0.00000000e+00, ...,
6.32747828e+00, 8.12373257e+00, 4.66672027e+00],
[2.82358995e+00, 4.33238434e+00, 2.53716630e-03, ...,
6.57664030e+00, 8.34962689e+00, 4.66190802e+00],
[2.83717001e+00, 4.22647197e+00, 9.19432870e-03, ...,
6.87448837e+00, 8.66938763e+00, 4.67183831e+00],
...,
[1.08623510e+01, 0.00000000e+00, 2.17196058e-02, ...,
3.69661552e+00, 7.05302934e+00, 6.81355294e+00],
[1.08496465e+01, 0.00000000e+00, 1.81035530e-02, ...,
3.27034629e+00, 6.49292639e+00, 6.29902832e+00],
[1.07398737e+01, 0.00000000e+00, 1.43236629e-02, ...,
2.90324026e+00, 6.04882393e+00, 5.83036094e+00]]),
array([[ 2.11831784, 10.69419042, 0.21505423, ..., 5.07913508,
8.94422957, 2.63084358],
[ 2.16348177, 10.45795399, 0.24262466, ..., 5.3451092 ,
9.03443795, 2.53770534],
[ 2.18308878, 10.17072963, 0.27470865, ..., 5.67611045,
9.16097271, 2.49429468],
...,
[ 8.8247157 , 0. , 0.0367272 , ..., 1.8818035 ,
4.6293494 , 9.0259091 ],
[ 8.4390372 , 0. , 0.02474601, ..., 1.88137858,
4.4051204 , 8.88185163],
[ 7.98817245, 0. , 0.01309776, ..., 1.86527967,
4.17928903, 8.81192185]]),
array([[3.39629665e+00, 7.00463819e+00, 0.00000000e+00, ...,
5.28191136e+00, 6.12543648e+00, 2.91734980e+00],
[3.46011408e+00, 6.69053997e+00, 2.53716630e-03, ...,
5.51170708e+00, 6.04945897e+00, 3.07804423e+00],
[3.50061814e+00, 6.21685457e+00, 9.19432870e-03, ...,
5.76270515e+00, 6.07062752e+00, 3.38514438e+00],
...,
[1.39221921e+01, 2.33137605e-01, 2.17196058e-02, ...,
1.70014312e+00, 4.54590576e+00, 1.41181193e+01],
[1.33655870e+01, 1.97628563e-01, 1.81035530e-02, ...,
1.72830456e+00, 4.64804468e+00, 1.40310547e+01],
[1.27224701e+01, 1.67153771e-01, 1.43236629e-02, ...,
1.73559402e+00, 4.69277745e+00, 1.39176802e+01]]),
array([[2.92818873e+00, 8.88511777e+00, 0.00000000e+00, ...,
6.08230196e+00, 6.32559883e+00, 4.02829268e+00],
[2.95725184e+00, 8.67118431e+00, 2.53716630e-03, ...,
6.37969174e+00, 6.23034686e+00, 4.21944934e+00],
[2.95555665e+00, 8.35423800e+00, 9.19432870e-03, ...,
6.69593092e+00, 6.21914291e+00, 4.50072967e+00],
...,
[1.31855439e+01, 0.00000000e+00, 2.17196058e-02, ...,
1.22244730e+00, 4.85320541e+00, 1.48812146e+01],
[1.25215927e+01, 0.00000000e+00, 1.81035530e-02, ...,
1.29120900e+00, 4.89898753e+00, 1.47732107e+01],
[1.17752762e+01, 0.00000000e+00, 1.43236629e-02, ...,
1.33721804e+00, 4.89353910e+00, 1.45994571e+01]]),
array([[2.1661972 , 2.5235727 , 0.27751269, ..., 4.69057111, 7.93697833,
3.59930798],
[2.18486393, 2.52532536, 0.27881646, ..., 4.82509464, 8.21048353,
3.66142442],
[2.22452177, 2.47239791, 0.28409345, ..., 5.00727729, 8.56381165,
3.79576044],
...,
[0.34041494, 2.02875002, 0. , ..., 1.4434876 , 5.42089901,
5.39462102],
[0.29190025, 2.00812064, 0. , ..., 1.44441935, 5.15215546,
5.06709833],
[0.28235252, 1.99189339, 0. , ..., 1.46256851, 4.90635372,
4.85216018]]),
array([[4.38094072, 1.34786396, 0.13763296, ..., 2.49438556, 6.78491403,
3.80264262],
[4.50959886, 1.30630662, 0.15525052, ..., 2.60091092, 7.02911298,
3.76431376],
[4.68635402, 1.23683753, 0.17954843, ..., 2.81844402, 7.36940474,
3.75646871],
...,
[4.20833187, 0.82642126, 0.05377715, ..., 3.05182198, 5.4383248 ,
7.08909981],
[4.12397487, 0.8117322 , 0.04669348, ..., 2.71974603, 5.34879127,
7.04697162],
[4.03982124, 0.79767332, 0.04127021, ..., 2.44698875, 5.22422725,
6.98704441]]),
array([[4.38637327, 3.50000409, 0.03681084, ..., 5.12879799, 5.13639474,
4.43479535],
[4.49722209, 3.44707267, 0. , ..., 5.40471333, 5.35645847,
4.53196139],
[4.66072004, 3.32217822, 0. , ..., 5.72045168, 5.70216571,
4.69152173],
...,
[3.75961589, 1.47985399, 0. , ..., 2.64707505, 4.32836776,
6.27973819],
[3.76004006, 1.46930674, 0. , ..., 2.44136646, 4.51775604,
5.64400466],
[3.78102941, 1.46087087, 0. , ..., 2.2445324 , 4.62990181,
5.12516763]]),
array([[ 1.67284766, 3.78310941, 1.34461666, ..., 6.64526805,
9.66530357, 4.36192764],
[ 1.62601009, 3.79168152, 1.31400528, ..., 6.92963131,
9.86429654, 4.36435343],
[ 1.57377631, 3.74955393, 1.28322386, ..., 7.2400401 ,
10.08464521, 4.37598207],
...,
[ 4.92935082, 0.88325087, 0. , ..., 0.85475323,
3.48216632, 5.43756607],
[ 4.97123288, 0.8454362 , 0. , ..., 0.9587218 ,
3.35247083, 5.11855388],
[ 5.0329417 , 0.81946136, 0. , ..., 1.05341164,
3.18709978, 4.82700983]]),
array([[ 0.99412432, 4.8576627 , 0.41105709, ..., 7.87827589,
10.57115949, 4.37378964],
[ 0.92491034, 4.74441713, 0.35794296, ..., 8.16607315,
10.8166572 , 4.31831125],
[ 0.85592805, 4.58619942, 0.30297457, ..., 8.45338379,
11.11853786, 4.24114624],
...,
[ 2.41458238, 0.91065277, 0.25655941, ..., 1.05618391,
4.8404833 , 5.71858979],
[ 2.9340891 , 0.89234805, 0.28052707, ..., 1.14284711,
4.54196809, 5.64482516],
[ 3.51260809, 0.87418824, 0.3151522 , ..., 1.22419 ,
4.22941372, 5.55370042]]),
array([[1.63247861, 5.37268842, 0.04003896, ..., 5.89955253, 7.92202996,
3.90887513],
[1.54792453, 5.24590515, 0.03223027, ..., 6.12136341, 8.07823884,
3.9661222 ],
[1.48386335, 5.02671679, 0.02696348, ..., 6.40447895, 8.27045225,
4.05843654],
...,
[2.53151947, 1.71243148, 0.04248903, ..., 1.25243942, 2.34441258,
5.2479366 ],
[3.34172802, 1.6931153 , 0.0280941 , ..., 1.25729113, 2.29428795,
5.48380539],
[4.24959854, 1.67676797, 0.0183203 , ..., 1.28376154, 2.2733006 ,
5.67726384]]),
array([[ 3.03184698, 18.19051296, 0.02552699, ..., 4.86427384,
8.99050183, 4.45005706],
[ 3.04883382, 17.81001742, 0.02841429, ..., 5.02831042,
9.13128015, 4.55174229],
[ 3.06969161, 17.18216759, 0.03587687, ..., 5.26834167,
9.31502294, 4.65313397],
...,
[ 9.16915401, 0.36555593, 0. , ..., 2.2002979 ,
5.22188172, 6.88591782],
[ 9.22802914, 0.3876448 , 0. , ..., 2.22215568,
4.99499157, 6.82857821],
[ 9.26775192, 0.42019963, 0. , ..., 2.23403637,
4.73964451, 6.83331492]]),
array([[3.45888483e+00, 1.33433515e+01, 0.00000000e+00, ...,
4.64597508e+00, 8.47134784e+00, 4.26172369e+00],
[3.44282061e+00, 1.30802485e+01, 2.53716630e-03, ...,
4.80456913e+00, 8.63707514e+00, 4.13004876e+00],
[3.43120538e+00, 1.27721680e+01, 9.19432870e-03, ...,
5.04747755e+00, 8.88052890e+00, 3.95978156e+00],
...,
[1.09010035e+01, 4.74113707e-01, 2.17196058e-02, ...,
1.14869158e+00, 6.34260349e+00, 5.55917430e+00],
[1.07766459e+01, 4.49853643e-01, 1.81035530e-02, ...,
1.29143872e+00, 5.94902133e+00, 4.93485098e+00],
[1.06362968e+01, 4.30287939e-01, 1.43236629e-02, ...,
1.42506227e+00, 5.59734139e+00, 4.45018623e+00]]),
array([[3.59303699e+00, 1.36376132e+01, 0.00000000e+00, ...,
4.67695396e+00, 6.74986331e+00, 4.29853963e+00],
[3.59911852e+00, 1.33614176e+01, 2.53716630e-03, ...,
4.79942996e+00, 6.81525250e+00, 4.24087208e+00],
[3.60176847e+00, 1.29664756e+01, 9.19432870e-03, ...,
5.00080124e+00, 6.96547774e+00, 4.16197421e+00],
...,
[1.24119090e+01, 1.01097213e+00, 2.17196058e-02, ...,
7.85695175e-01, 4.86564806e+00, 5.24116755e+00],
[1.21151192e+01, 9.62014863e-01, 1.81035530e-02, ...,
9.89602689e-01, 4.80097330e+00, 4.71250606e+00],
[1.17685798e+01, 9.22474453e-01, 1.43236629e-02, ...,
1.18517990e+00, 4.72085365e+00, 4.36203982e+00]]),
array([[3.83690411e+00, 3.01324473e+01, 0.00000000e+00, ...,
6.45954620e+00, 1.00985423e+01, 4.04038690e+00],
[3.80690531e+00, 2.95470671e+01, 0.00000000e+00, ...,
6.73224780e+00, 1.04342271e+01, 4.05965009e+00],
[3.77360588e+00, 2.88660519e+01, 0.00000000e+00, ...,
7.02779529e+00, 1.08846376e+01, 4.13359498e+00],
...,
[1.48139660e+01, 0.00000000e+00, 2.28058012e-02, ...,
2.48588666e+00, 8.68580680e+00, 1.19128188e+01],
[1.47507998e+01, 0.00000000e+00, 2.01942520e-02, ...,
2.48328402e+00, 8.22786119e+00, 1.09379110e+01],
[1.46854196e+01, 0.00000000e+00, 1.81018487e-02, ...,
2.44746309e+00, 7.70270701e+00, 1.01114261e+01]]),
array([[4.16262155e+00, 1.33158070e+01, 2.66459135e-02, ...,
4.67075948e+00, 7.75591225e+00, 5.40562174e+00],
[4.02922599e+00, 1.30320370e+01, 3.06346476e-02, ...,
4.92589047e+00, 7.85186725e+00, 5.50559104e+00],
[3.86049775e+00, 1.25184081e+01, 3.60075809e-02, ...,
5.19227871e+00, 8.08240259e+00, 5.65126643e+00],
...,
[2.62708129e+01, 9.57655412e-01, 3.22425779e-03, ...,
1.85271185e+00, 7.25946058e+00, 1.85697925e+01],
[2.64174054e+01, 9.36369282e-01, 0.00000000e+00, ...,
1.85983944e+00, 7.08218548e+00, 1.74764932e+01],
[2.64651754e+01, 9.27900269e-01, 0.00000000e+00, ...,
1.83158144e+00, 6.84042555e+00, 1.63048872e+01]]),
array([[4.81486559e+00, 9.87981058e+00, 0.00000000e+00, ...,
3.43231458e+00, 6.38913878e+00, 3.70414895e+00],
[4.75473338e+00, 9.54333934e+00, 2.53716630e-03, ...,
3.64199351e+00, 6.43780807e+00, 3.74391613e+00],
[4.66258347e+00, 9.15017896e+00, 9.19432870e-03, ...,
3.90434861e+00, 6.60395858e+00, 3.87585213e+00],
...,
[2.68888276e+01, 7.66918045e-01, 2.17196058e-02, ...,
1.77040600e+00, 7.44149579e+00, 1.92274424e+01],
[2.67978171e+01, 7.15036519e-01, 1.81035530e-02, ...,
1.74380444e+00, 7.23225781e+00, 1.90728108e+01],
[2.65891865e+01, 6.57957187e-01, 1.43236629e-02, ...,
1.70214068e+00, 6.99869161e+00, 1.87246751e+01]]),
array([[1.67174264, 2.43959536, 1.38538653, ..., 4.74685287, 7.31034704,
4.80007175],
[1.6111994 , 2.4414976 , 1.38506981, ..., 4.93464215, 7.59937403,
4.83467302],
[1.55285373, 2.40422794, 1.43514828, ..., 5.19880838, 7.91017006,
4.88803893],
...,
[4.78349357, 0.9658223 , 0.03373824, ..., 0.91599197, 2.94042606,
5.37951094],
[5.15032037, 0.9167522 , 0.02013679, ..., 0.93846803, 2.92093897,
4.67229156],
[5.55156386, 0.87893479, 0.01382974, ..., 0.98713214, 2.88443753,
4.0580335 ]]),
array([[3.60293753e+00, 5.57110984e+00, 4.24804875e-02, ...,
3.33662223e+00, 6.38483670e+00, 3.37936386e+00],
[3.70620919e+00, 5.53014842e+00, 4.62492253e-02, ...,
3.39525585e+00, 6.59610920e+00, 3.42988599e+00],
[3.75974752e+00, 5.44068683e+00, 4.87989165e-02, ...,
3.56151364e+00, 6.89272912e+00, 3.57635606e+00],
...,
[2.03940376e+01, 2.24743424e+00, 6.41023131e-03, ...,
4.77047485e+00, 4.45593648e+00, 8.26459937e+00],
[1.96912774e+01, 1.99264393e+00, 2.84434305e-03, ...,
4.16803418e+00, 4.48251246e+00, 8.49483508e+00],
[1.87424474e+01, 1.77347861e+00, 0.00000000e+00, ...,
3.66423079e+00, 4.46146892e+00, 8.61579689e+00]]),
array([[4.48606190e+00, 3.36537667e+00, 5.44747418e-03, ...,
3.46376010e+00, 6.16735995e+00, 2.54739909e+00],
[4.63929197e+00, 3.36762284e+00, 1.53812176e-02, ...,
3.52081867e+00, 6.34841022e+00, 2.60437515e+00],
[4.75963250e+00, 3.39595169e+00, 2.28532473e-02, ...,
3.70965668e+00, 6.61248367e+00, 2.78285954e+00],
...,
[2.42119706e+01, 3.17126577e+00, 3.09260242e-02, ...,
7.36132789e+00, 3.84497885e+00, 6.71261176e+00],
[2.42757677e+01, 2.84246759e+00, 2.68575739e-02, ...,
6.31567700e+00, 3.91876337e+00, 7.05351891e+00],
[2.40203684e+01, 2.55401811e+00, 2.29710782e-02, ...,
5.41976158e+00, 3.95396546e+00, 7.38299038e+00]]),
array([[ 1.70134116, 5.6116097 , 0.11133268, ..., 4.78765838,
10.21658062, 5.39524485],
[ 1.6854092 , 5.53368572, 0.13181389, ..., 5.07415588,
10.32989929, 5.36677006],
[ 1.64716838, 5.40067383, 0.15416966, ..., 5.395865 ,
10.4240818 , 5.27879445],
...,
[ 8.98838016, 0.25537174, 0.07603432, ..., 1.68785227,
2.19851495, 6.57151886],
[ 9.06553622, 0.25267944, 0.07104552, ..., 1.6818297 ,
1.97559738, 6.35830153],
[ 9.06332419, 0.25738245, 0.06729679, ..., 1.65127335,
1.79747874, 6.08655866]]),
array([[ 1.9514751 , 11.25891276, 0. , ..., 4.23848279,
6.75870998, 3.60931407],
[ 1.9390338 , 11.04312885, 0. , ..., 4.3585828 ,
6.8952171 , 3.62783242],
[ 1.90191424, 10.66768059, 0. , ..., 4.5551933 ,
7.1370725 , 3.64516701],
...,
[ 6.15278419, 0.44162324, 0.20153968, ..., 4.18000531,
5.43747847, 4.91493014],
[ 5.38906925, 0.44928765, 0.20844029, ..., 3.81328891,
5.45464084, 5.37732822],
[ 4.70250957, 0.46824083, 0.21886644, ..., 3.48552942,
5.38905539, 5.8080965 ]]),
array([[ 1.97153221, 11.46231957, 0. , ..., 5.5101095 ,
5.59557538, 4.61537225],
[ 1.94054883, 11.21265552, 0. , ..., 5.62768543,
5.72792101, 4.74557023],
[ 1.8952984 , 10.94393417, 0. , ..., 5.78694283,
6.02259949, 4.86975252],
...,
[ 3.64269152, 0. , 0.23500717, ..., 4.37391474,
5.38156944, 6.44316101],
[ 2.81507962, 0. , 0.23250367, ..., 4.02819368,
5.45667659, 6.65390867],
[ 2.12866118, 0. , 0.23555779, ..., 3.71381023,
5.4806318 , 6.8613414 ]]),
array([[2.05982834, 3.55315018, 0.02431112, ..., 4.6352684 , 7.54791175,
4.38159168],
[2.10382514, 3.55145146, 0.01780008, ..., 4.84141765, 7.70290058,
4.41342408],
[2.16392467, 3.4808129 , 0.02475069, ..., 5.102272 , 7.96484493,
4.47150792],
...,
[0.4983875 , 1.03505283, 0.03059421, ..., 1.56252294, 5.19455662,
6.67031464],
[0.41750924, 1.03299587, 0.03364938, ..., 1.53423549, 5.1337303 ,
6.36873127],
[0.34947668, 1.03932293, 0.03888785, ..., 1.51362945, 5.02518762,
6.08087758]]),
array([[2.3835189 , 5.48120158, 0.09453257, ..., 4.4543095 , 6.37686628,
3.03691431],
[2.41877755, 5.39777116, 0.11964056, ..., 4.68202098, 6.54633137,
2.97125027],
[2.49025207, 5.20994187, 0.14240104, ..., 4.9329246 , 6.78412569,
2.96803844],
...,
[0. , 5.27189519, 0.04822969, ..., 1.5570349 , 4.28810627,
7.16803797],
[0.17076424, 5.20916718, 0.03978519, ..., 1.58762256, 4.07315739,
7.04921905],
[0.60095771, 5.14482828, 0.03131174, ..., 1.59278208, 3.94580987,
6.97517439]]),
array([[1.68019441e+00, 4.34201956e+00, 0.00000000e+00, ...,
4.08505276e+00, 7.74966418e+00, 3.08845590e+00],
[1.69190550e+00, 4.24427050e+00, 2.53716630e-03, ...,
4.30113748e+00, 8.07153916e+00, 3.06324689e+00],
[1.72129162e+00, 4.12280557e+00, 9.19432870e-03, ...,
4.54031319e+00, 8.46263140e+00, 3.11714767e+00],
...,
[9.07808269e-01, 4.02408239e+00, 2.17196058e-02, ...,
1.74685036e+00, 7.11249436e+00, 7.01093667e+00],
[1.33485468e+00, 3.95265906e+00, 1.81035530e-02, ...,
1.76927877e+00, 6.60604206e+00, 6.91223411e+00],
[1.77117647e+00, 3.88218905e+00, 1.43236629e-02, ...,
1.76052251e+00, 6.17114431e+00, 6.87694557e+00]]),
array([[2.24393100e+00, 1.47794056e+01, 1.89424935e-02, ...,
6.11974872e+00, 9.26545829e+00, 3.28014172e+00],
[2.27549767e+00, 1.44999369e+01, 2.42367198e-02, ...,
6.44984455e+00, 9.24959916e+00, 3.29530440e+00],
[2.28396850e+00, 1.40474917e+01, 2.96305044e-02, ...,
6.80377501e+00, 9.22861427e+00, 3.35122880e+00],
...,
[9.00328976e+00, 6.88677185e-01, 8.07273616e-03, ...,
2.06826476e+00, 4.07065056e+00, 7.48004349e+00],
[8.60092752e+00, 6.97498071e-01, 3.50362442e-03, ...,
2.07396814e+00, 3.88006245e+00, 7.58312824e+00],
[8.14321780e+00, 7.18219039e-01, 0.00000000e+00, ...,
2.04189170e+00, 3.67310366e+00, 7.69418279e+00]]),
array([[ 2.63004293, 13.15054245, 0.09711463, ..., 6.94348215,
8.11508685, 3.67999824],
[ 2.64710021, 12.83505346, 0.09139821, ..., 7.17856527,
8.18833389, 3.6659022 ],
[ 2.67520423, 12.47671897, 0.0879107 , ..., 7.42807873,
8.30170072, 3.66647328],
...,
[ 4.90074016, 0.6410302 , 0. , ..., 0.90121902,
4.1719555 , 7.99149385],
[ 4.7924782 , 0.57817534, 0. , ..., 1.14899621,
4.08015955, 7.74954519],
[ 4.66974407, 0.52326115, 0. , ..., 1.35464352,
3.95994785, 7.62596348]]),
array([[ 2.2531288 , 13.11517962, 0.02274553, ..., 5.94163294,
8.37941539, 4.20620757],
[ 2.26076089, 12.88201834, 0.03129889, ..., 6.13645628,
8.38773498, 4.15189449],
[ 2.27240023, 12.57959067, 0.03784419, ..., 6.35989021,
8.40229213, 4.08854187],
...,
[ 4.35778433, 1.10009666, 0.03987867, ..., 0.83875578,
2.71887398, 7.97068796],
[ 4.15192693, 1.05363283, 0.03594699, ..., 1.07753434,
2.62201918, 7.27308466],
[ 3.91167358, 1.01638026, 0.03260308, ..., 1.2801305 ,
2.54708774, 6.73945067]]),
array([[4.00858119e+00, 3.24667273e+01, 0.00000000e+00, ...,
5.51903149e+00, 8.31040594e+00, 5.07776173e+00],
[3.99378711e+00, 3.18997727e+01, 2.53716630e-03, ...,
5.81823402e+00, 8.69463831e+00, 4.91123461e+00],
[3.97015608e+00, 3.11306913e+01, 9.19432870e-03, ...,
6.21668276e+00, 9.19759666e+00, 4.70863538e+00],
...,
[1.62127227e+01, 6.04063832e-02, 2.17196058e-02, ...,
2.33801702e+00, 7.82546582e+00, 1.26572846e+01],
[1.60127366e+01, 8.20528095e-02, 1.81035530e-02, ...,
2.28502341e+00, 7.39859480e+00, 1.09883642e+01],
[1.57853376e+01, 1.17971467e-01, 1.43236629e-02, ...,
2.22443323e+00, 6.97296503e+00, 9.52077959e+00]]),
array([[4.59636253e+00, 1.51228032e+01, 0.00000000e+00, ...,
5.79748710e+00, 8.35883378e+00, 4.28791577e+00],
[4.52867166e+00, 1.47691628e+01, 0.00000000e+00, ...,
6.11891130e+00, 8.38398476e+00, 4.38628866e+00],
[4.41620591e+00, 1.41501404e+01, 0.00000000e+00, ...,
6.44243657e+00, 8.46526082e+00, 4.58615337e+00],
...,
[2.96415667e+01, 1.10444900e+00, 4.60976007e-03, ...,
2.18870430e+00, 7.34412075e+00, 2.39808256e+01],
[2.97225981e+01, 1.08855059e+00, 3.28610127e-03, ...,
2.13545699e+00, 6.98121979e+00, 2.31699312e+01],
[2.96368084e+01, 1.08261995e+00, 2.04614425e-03, ...,
2.04906931e+00, 6.60126727e+00, 2.21936871e+01]]),
array([[4.74403555e+00, 1.52439367e+01, 0.00000000e+00, ...,
4.48828062e+00, 7.36174411e+00, 4.71413619e+00],
[4.70133414e+00, 1.47983994e+01, 2.53716630e-03, ...,
4.72801597e+00, 7.41621859e+00, 4.76905247e+00],
[4.62126209e+00, 1.41699396e+01, 9.19432870e-03, ...,
4.98328176e+00, 7.55128599e+00, 4.86602547e+00],
...,
[2.62973034e+01, 7.35078780e-01, 2.17196058e-02, ...,
1.89411275e+00, 7.06295086e+00, 1.91460362e+01],
[2.59438903e+01, 7.09686750e-01, 1.81035530e-02, ...,
1.90406942e+00, 6.86475533e+00, 1.87175930e+01],
[2.54743911e+01, 6.79244603e-01, 1.43236629e-02, ...,
1.87894187e+00, 6.60764332e+00, 1.80835124e+01]]),
array([[1.97422741, 2.38783835, 0.42322415, ..., 3.2127826 , 7.869418 ,
3.78621434],
[2.00308382, 2.35050463, 0.44421538, ..., 3.36643677, 8.06688537,
3.85497313],
[2.04269174, 2.29734954, 0.49496963, ..., 3.59872044, 8.33313342,
3.99132756],
...,
[1.44845741, 1.54287165, 0.07724476, ..., 1.49748927, 4.99536572,
6.3051305 ],
[1.37473172, 1.51138651, 0.06266573, ..., 1.46209031, 4.83799339,
6.17096632],
[1.31491507, 1.48430523, 0.0530803 , ..., 1.44056247, 4.66360984,
6.09286264]]),
array([[3.94394704, 3.93257544, 0. , ..., 6.17684501, 5.96283743,
3.95408926],
[4.05711065, 3.82142316, 0. , ..., 6.3950154 , 6.19994984,
3.94489489],
[4.20180031, 3.61165135, 0. , ..., 6.66180343, 6.54214899,
3.958892 ],
...,
[6.1202223 , 2.64841569, 0.6230479 , ..., 5.2232439 , 4.7492793 ,
5.35138759],
[6.07401185, 2.6137153 , 0.68437808, ..., 4.58533579, 4.76050779,
5.36996563],
[5.99550454, 2.58396006, 0.76123947, ..., 4.02262358, 4.73998794,
5.39107743]]),
array([[4.12986839, 6.4913873 , 0.22868276, ..., 4.34802236, 6.61727375,
4.61104453],
[4.22044088, 6.31776952, 0.24556686, ..., 4.50874806, 6.81464986,
4.66799884],
[4.3535659 , 6.01535579, 0.26648252, ..., 4.77429244, 7.09921205,
4.7366995 ],
...,
[5.40723976, 3.28316801, 0.13025596, ..., 5.44040271, 4.47465323,
6.29153047],
[5.49656205, 3.23768612, 0.12687049, ..., 4.72819993, 4.58534355,
6.2952054 ],
[5.58692604, 3.1980471 , 0.12690917, ..., 4.11358187, 4.59866534,
6.27492379]]),
array([[2.13396784, 2.20113094, 0.136431 , ..., 5.68870401, 5.99544453,
4.33625569],
[2.16594695, 2.16071201, 0.12639135, ..., 5.97966491, 6.25539887,
4.40302177],
[2.21821366, 2.07971905, 0.12936876, ..., 6.27754827, 6.60989658,
4.51553512],
...,
[0.10985587, 2.28914973, 0. , ..., 1.36497315, 4.44881146,
5.43796407],
[0.0401704 , 2.25625577, 0. , ..., 1.41480045, 4.27535006,
4.79665301],
[0. , 2.22771254, 0. , ..., 1.43584947, 4.17678356,
4.28862017]]),
array([[4.37317413, 4.53820267, 0.15455207, ..., 6.06036476, 5.86743565,
4.35083265],
[4.49454727, 4.51582299, 0.17028971, ..., 6.36131612, 6.07608099,
4.46587467],
[4.65902769, 4.39051118, 0.2022707 , ..., 6.68927476, 6.37555311,
4.64074303],
...,
[5.36186128, 0.92327553, 0.30878925, ..., 2.83115382, 5.24944865,
6.29573774],
[5.26566452, 0.93236363, 0.32664867, ..., 2.59146775, 5.23305874,
5.93384769],
[5.15772764, 0.9464536 , 0.35144171, ..., 2.3658779 , 5.17456636,
5.66772745]]),
array([[3.78697873, 4.72092258, 0. , ..., 4.86341036, 6.27067703,
4.33081914],
[3.87025014, 4.53797101, 0. , ..., 5.15396468, 6.52275546,
4.43755335],
[3.99047086, 4.28484563, 0. , ..., 5.48451351, 6.86594672,
4.60175004],
...,
[3.40578233, 2.52517943, 0.02483981, ..., 2.5318884 , 4.32702386,
7.44492801],
[3.15031481, 2.48341153, 0.02296706, ..., 2.32764231, 4.37059484,
7.22186744],
[2.91565347, 2.44423286, 0.02158778, ..., 2.12939584, 4.36670433,
7.02386729]]),
array([[1.76857594, 1.91376944, 0.45307885, ..., 4.99054688, 6.01567197,
3.98106175],
[1.77033674, 1.89129592, 0.44970248, ..., 5.22395287, 6.09303556,
4.01107057],
[1.78052485, 1.84123543, 0.47529364, ..., 5.48773383, 6.24091612,
4.09208138],
...,
[1.08205022, 1.21927536, 0.01061059, ..., 1.63152627, 3.2850001 ,
4.67774648],
[0.96708528, 1.18982828, 0. , ..., 1.61599287, 3.46980221,
4.3926373 ],
[0.87434741, 1.16771765, 0. , ..., 1.59301522, 3.58590972,
4.13722161]]),
array([[2.16984876, 4.48525848, 0.17476391, ..., 5.06111847, 8.1032136 ,
4.20299582],
[2.19506273, 4.38331281, 0.16769719, ..., 5.2329397 , 8.39595045,
4.22925919],
[2.23148794, 4.28299785, 0.15406224, ..., 5.45956587, 8.7735848 ,
4.2772233 ],
...,
[6.44960573, 1.76321386, 0.08150546, ..., 1.68716222, 4.98722882,
5.42716419],
[7.36065084, 1.73093303, 0.04830251, ..., 1.65305933, 4.76275138,
5.48425416],
[8.29885561, 1.69946206, 0.02292283, ..., 1.63654123, 4.552753 ,
5.51030344]]),
array([[1.71497468e+00, 6.31838685e+00, 0.00000000e+00, ...,
6.32488962e+00, 7.57468653e+00, 4.52793954e+00],
[1.64326007e+00, 6.21976775e+00, 0.00000000e+00, ...,
6.65748308e+00, 7.79952800e+00, 4.46883335e+00],
[1.57361560e+00, 6.03587880e+00, 0.00000000e+00, ...,
7.02185504e+00, 8.14917665e+00, 4.36331392e+00],
...,
[6.76200730e+00, 1.87959685e+00, 2.35140935e-02, ...,
1.51148048e+00, 4.81847151e+00, 4.27912940e+00],
[7.54633061e+00, 1.85902532e+00, 3.11131938e-03, ...,
1.49796117e+00, 4.71365140e+00, 4.41783148e+00],
[8.39558608e+00, 1.84417967e+00, 0.00000000e+00, ...,
1.47489105e+00, 4.60438333e+00, 4.51663551e+00]]),
array([[2.31002186e+00, 1.07825307e+01, 1.45709582e-01, ...,
6.51597704e+00, 7.41970030e+00, 2.97310509e+00],
[2.38012619e+00, 1.05464839e+01, 1.56103935e-01, ...,
6.87920709e+00, 7.54717898e+00, 2.93804823e+00],
[2.42339477e+00, 1.02476466e+01, 1.60117137e-01, ...,
7.26725402e+00, 7.72874314e+00, 2.94825256e+00],
...,
[9.87634695e+00, 2.93613147e-01, 1.56878043e-02, ...,
1.77420911e+00, 3.88191946e+00, 3.81132648e+00],
[9.49697922e+00, 2.87768803e-01, 1.23756708e-02, ...,
1.81666299e+00, 3.77174619e+00, 3.43366257e+00],
[9.02746987e+00, 2.85962281e-01, 8.72620507e-03, ...,
1.81817501e+00, 3.67745644e+00, 3.29885198e+00]]),
array([[3.21277515e+00, 1.24474688e+01, 0.00000000e+00, ...,
7.80131872e+00, 1.08301836e+01, 4.04235072e+00],
[3.26720452e+00, 1.22425491e+01, 2.53716630e-03, ...,
8.04026552e+00, 1.08924916e+01, 4.09210579e+00],
[3.34094458e+00, 1.19442613e+01, 9.19432870e-03, ...,
8.26612675e+00, 1.09810290e+01, 4.14701895e+00],
...,
[4.87413482e+00, 0.00000000e+00, 2.17196058e-02, ...,
1.19605675e+00, 5.28689707e+00, 9.92913314e+00],
[4.64222428e+00, 0.00000000e+00, 1.81035530e-02, ...,
1.43702064e+00, 4.89903843e+00, 1.01372313e+01],
[4.41654794e+00, 0.00000000e+00, 1.43236629e-02, ...,
1.62903346e+00, 4.51813033e+00, 1.02985446e+01]]),
array([[ 3.11344004, 12.46189015, 0.02772509, ..., 6.80644969,
9.06736874, 3.90180133],
[ 3.15640443, 12.20726933, 0.04160669, ..., 6.9821497 ,
8.98179516, 3.90316852],
[ 3.22049525, 11.93796023, 0.05277182, ..., 7.16108983,
8.91494932, 3.92174157],
...,
[ 4.23114269, 0.27683873, 0.0575708 , ..., 1.53946484,
4.87649074, 7.29790621],
[ 4.00087071, 0.2387514 , 0.05481406, ..., 1.71666283,
4.76616928, 6.80951323],
[ 3.76740791, 0.20743961, 0.05251282, ..., 1.8589403 ,
4.58198085, 6.47131632]]),
array([[1.53520051, 4.59404561, 0.69650994, ..., 4.6652168 , 7.7706666 ,
3.71935325],
[1.49356376, 4.62075778, 0.75640675, ..., 4.75847938, 8.02766997,
3.670165 ],
[1.45206869, 4.59225149, 0.84382598, ..., 4.92248226, 8.3239652 ,
3.66381708],
...,
[3.04199233, 1.04870198, 0.15385666, ..., 0.61562018, 3.23333672,
5.53329184],
[3.10889551, 1.01196608, 0.13424563, ..., 0.73029641, 3.17196098,
4.98010311],
[3.20311514, 0.98977805, 0.11862781, ..., 0.87228855, 3.1032025 ,
4.54317915]]),
array([[ 1.88972309, 9.17517381, 0.13348495, ..., 5.57425973,
9.71933929, 3.9532184 ],
[ 1.83549704, 9.06455493, 0.08798494, ..., 5.78269283,
9.95784773, 3.95449933],
[ 1.79743651, 8.90205485, 0.04709913, ..., 6.03073551,
10.23432308, 3.97450476],
...,
[ 3.69991859, 0.82953324, 0. , ..., 1.18572003,
4.36306046, 4.53854002],
[ 4.34898337, 0.81648911, 0. , ..., 1.22989548,
4.24057743, 4.4180756 ],
[ 5.08251165, 0.81189869, 0. , ..., 1.27918417,
4.04256377, 4.35756982]]),
array([[ 2.06554123, 6.18537404, 0.06868147, ..., 3.57369853,
10.15436423, 4.29274563],
[ 2.04751501, 6.09363922, 0.0518833 , ..., 3.73498005,
10.42118666, 4.25516171],
[ 2.04551634, 5.85653196, 0.03305173, ..., 3.99129283,
10.68487807, 4.20883976],
...,
[ 4.47033693, 2.51625154, 0.02424907, ..., 1.38346883,
4.11185921, 3.28459443],
[ 5.19092824, 2.48853213, 0. , ..., 1.34324916,
3.8371583 , 2.99553942],
[ 5.98113628, 2.47290815, 0. , ..., 1.3295015 ,
3.54618785, 2.80586038]]),
array([[2.46287652, 3.25245862, 0.12168607, ..., 5.06595496, 6.63756555,
4.23676053],
[2.51827149, 3.20849835, 0.1294703 , ..., 5.30109212, 6.94258128,
4.34124277],
[2.6019945 , 3.11771282, 0.14742583, ..., 5.57130947, 7.36360535,
4.4895964 ],
...,
[0. , 1.41923997, 0.06113549, ..., 1.42824865, 5.96911824,
6.09373681],
[0. , 1.4011919 , 0.05727268, ..., 1.44332079, 5.81758357,
5.61914298],
[0. , 1.38900673, 0.05541362, ..., 1.45086154, 5.64973007,
5.2806425 ]]),
array([[1.1283109 , 3.72732308, 0.03317562, ..., 4.08434178, 7.98704752,
3.57730571],
[1.07401628, 3.67408496, 0.04209687, ..., 4.29024486, 8.2400712 ,
3.46852056],
[1.02082154, 3.57171438, 0.04908442, ..., 4.5438253 , 8.56850635,
3.38095036],
...,
[1.62773024, 2.00030449, 0.03265341, ..., 1.5264706 , 5.2175146 ,
7.28299232],
[1.73200003, 1.97452781, 0.02497668, ..., 1.51786737, 4.87984286,
7.02627609],
[1.79106034, 1.95285785, 0.01839627, ..., 1.50399782, 4.61014814,
6.79648345]]),
array([[2.15412789, 1.34814189, 0.27621233, ..., 4.71911224, 8.11097254,
2.61164005],
[2.1813918 , 1.31039605, 0.31358344, ..., 4.9602686 , 8.1979078 ,
2.57673621],
[2.22768334, 1.23655348, 0.34637494, ..., 5.22855979, 8.32726573,
2.65384469],
...,
[1.50099996, 3.92611469, 0.0766108 , ..., 1.60908892, 3.90096555,
8.00202838],
[1.59650011, 3.85414324, 0.05979798, ..., 1.62807999, 3.78877146,
7.72369301],
[1.68334604, 3.78309512, 0.04388734, ..., 1.62466173, 3.67344209,
7.53052016]]),
array([[ 4.47135775, 28.07050871, 0.05881318, ..., 5.25040788,
9.10934219, 4.40032477],
[ 4.53248333, 27.46785088, 0.05653304, ..., 5.52481732,
9.28146695, 4.38207769],
[ 4.59561374, 26.77239777, 0.05773507, ..., 5.87564411,
9.53314129, 4.35657564],
...,
[15.64284707, 0. , 0. , ..., 1.83179948,
5.193791 , 5.6583074 ],
[15.52282691, 0. , 0. , ..., 1.88077735,
5.00457638, 4.85246925],
[15.34645113, 0. , 0. , ..., 1.90491891,
4.77965455, 4.24236765]]),
array([[3.77340434e+00, 8.60491149e+00, 0.00000000e+00, ...,
4.40395695e+00, 7.52404721e+00, 3.63281784e+00],
[3.85673213e+00, 8.38078385e+00, 2.53716630e-03, ...,
4.61783086e+00, 7.50351614e+00, 3.44206820e+00],
[3.93039858e+00, 8.04547212e+00, 9.19432870e-03, ...,
4.90971440e+00, 7.50662560e+00, 3.25699962e+00],
...,
[1.28406137e+01, 0.00000000e+00, 2.17196058e-02, ...,
7.21028507e-01, 3.36880070e+00, 1.32955041e+01],
[1.24224972e+01, 0.00000000e+00, 1.81035530e-02, ...,
9.38760200e-01, 3.24690839e+00, 1.29036211e+01],
[1.19799399e+01, 0.00000000e+00, 1.43236629e-02, ...,
1.12317149e+00, 3.16452067e+00, 1.23950313e+01]]),
array([[4.79367478e+00, 9.72567097e+00, 0.00000000e+00, ...,
2.81425145e+00, 7.52085325e+00, 2.55881505e+00],
[4.97173763e+00, 9.44613190e+00, 2.53716630e-03, ...,
2.86060853e+00, 7.44644287e+00, 2.54471087e+00],
[5.16679166e+00, 9.05003080e+00, 9.19432870e-03, ...,
3.00095404e+00, 7.39437883e+00, 2.64470652e+00],
...,
[1.42206142e+01, 9.30888080e-01, 2.17196058e-02, ...,
1.13199235e+00, 4.76599983e+00, 1.33878178e+01],
[1.45671559e+01, 9.16308510e-01, 1.81035530e-02, ...,
1.33561520e+00, 4.76926291e+00, 1.32545969e+01],
[1.48746468e+01, 9.06497934e-01, 1.43236629e-02, ...,
1.51902492e+00, 4.68225627e+00, 1.31129016e+01]])]
print(len(times)) # Show the length of time
times[:10] # Look at the first 10 entries in time
61
[-50, -40, -30, -20, -10, 0, 10, 20, 30, 40]
The meaning of the times length is a bit trickier to derive from the paper, but the documentation for exampleMat.mat tells us that these times are in milliseconds (ms), and start 50 ms before the reach at time 0. A firing rate was sampled every 10 ms, so this is why these timestamps are 10 apart.
Visually explore the data#
Now that we understand the structure of the data, we can take a look at some of these trials. Below, we’ll create a firing rate plot for one trial at a time. In this plot, each neuron will be a different color.
Task: Change the value indexed in
data` below (keeping in mind how many conditions we have in total as well as 0 indexing in Python!) to look through a few different trials for patterns.trial = data[25] # You can change the index here if you'd like to look through different trials.
def plotFiringRates(times,trial):
plt.plot(times,trial)
plt.xlabel('Time (ms)')
plt.ylabel('Firing Rate (Hz)')
plt.vlines(0,np.min(trial),np.max(trial),color='gray',linestyle='--')
plt.show()
plotFiringRates(times,trial)
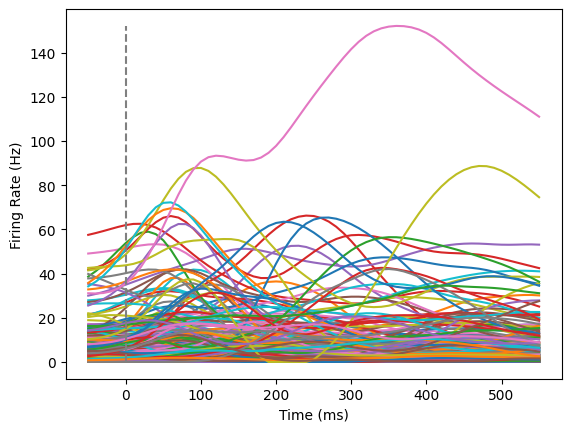
As you can appreciate from this plot, it is hard to make much sense of what this population of neurons are doing. Some neurons respond to the plotted condition, but not others.
We could investigate what happens if we average across all of the neurons, and then plot to compare trials against one another. In this plot, each line is a different condition.
all_trials = np.zeros((61,108))
for idx,this_trial in enumerate(data):
trial_average = np.mean(this_trial,axis=1)
all_trials[:,idx] = trial_average
plotFiringRates(times,all_trials)
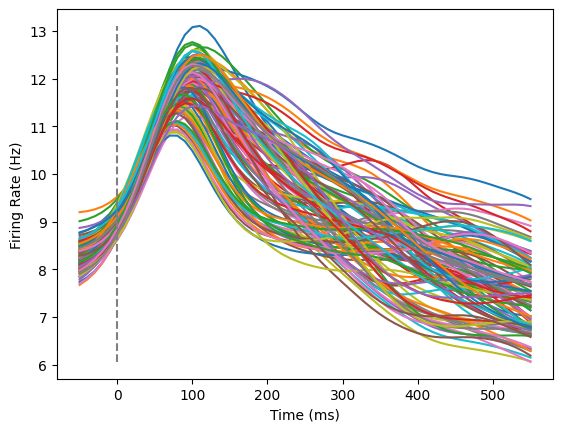
This is also not particularly informative! Clearly, neural activity increases overall when a monkey initiates a reach, but what does this tell us about neural coding?
Let’s do one final check, where we look at a single cell across multiple conditions. This is similar to Figure 2 of the paper, except we won’t color these by preparatory activity.
Task: Change the value of
neuron below (keeping in mind how many neurons we have in total as well as 0 indexing in Python!) to look through a few neurons for patterns.neuron = 200
trials_for_neuron = np.zeros((61,108))
for idx,this_trial in enumerate(data):
trials_for_neuron[:,idx] = this_trial[:,neuron]
plotFiringRates(times,trials_for_neuron)
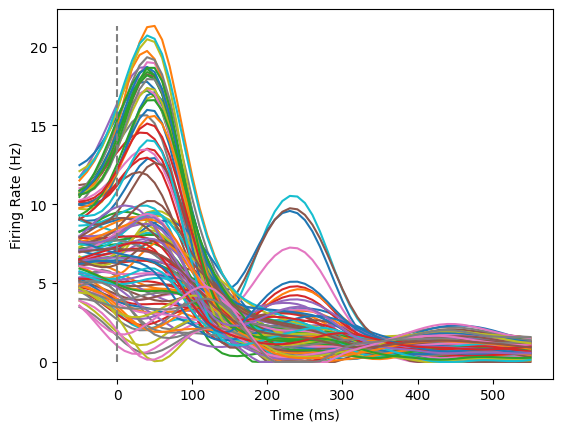
In summary, we can learn a few things away from the data exploration above:
Neural activity increases overall when the monkey reaches.
Individual neurons show different patterns of responses to reaches. Some neurons increase their firing rate to any reach, others are more selective. The timing of their firing rate variation also varies after the reach.
jPCA#
Okay, enough of the old school, simple analyses! Below, we’ll use jPCA to retain information from each individual neuron and each condition, looking at how each neuron moves through state space over time. To create our jPCA plot, we’ll use the jPCA package.
# Create a jPCA object
jpca = jPCA.JPCA(num_jpcs=6)
# Fit the jPCA object to data
projected, full_data_var, pca_var_capt, jpca_var_capt = jpca.fit(data, times=times, tstart=-50, tend=150)
# Plot the projected data
fig, axes = plt.subplots(1, 2, figsize=(10, 5))
plot_projections(projected, axis=axes[0], x_idx=0, y_idx=1) # Plot the first jPCA plane
plot_projections(projected, axis=axes[1], x_idx=2, y_idx=3) # Plot the second jPCA plane
axes[0].set_title('jPCA Plane 1')
axes[1].set_title('jPCA Plane 2')
plt.tight_layout()
plt.show()
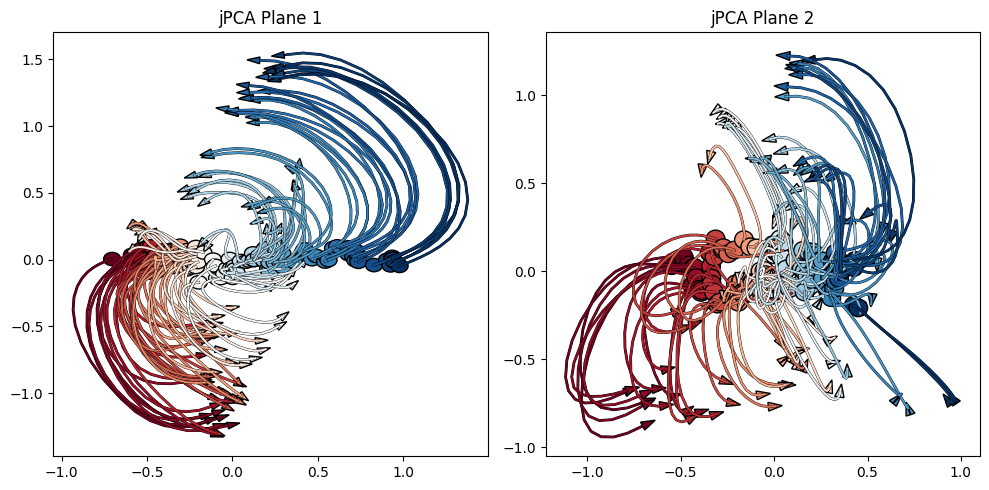
Above, we’ve generated figures really similar to Figure 3. However, the utility of working with this data live is that we can change features of the analysis and observe how this changes the plots (and our interpretation of the data).
Task: Try the following with the code:
By default, the jPCA is fit to -50 ms to 150 ms of the data. Change
tendto include more of the data in the analysis, and observe how this changes the PCA plots.Bonus: What dicates the coloring of the lines here? Dig into
utilsto find out.